PLC DASAR : MEMBUAT PROGRAM PLC DENGAN ALJABAR BOLE DAN MENYEDERHANAKAN LADDER DIAGRAM MENGGUNAKAN ALJABAR BOOLE

1. PENYEDERHANAAN LOGIKA LADDER

Jika kita melihat program ladder pada gambar 2.3 program terlihat begitu panjang dan berulang-ulang dalam menggunakan input dan output yang sama, dengan melakukan penyederhanaan logika maka dapat meminimalisir penggunaan jumlah input yang diulang-ulang. Berikut ini adalah metode penyederhanaan logika.

a. Aljabar Boole

Aljabar boole adalah matematika yang khusus digunakan untuk melakukan analisis terhadap Boolean ( bilangan yang hanya terdiri dari dua kondisi 0 dan 1). Berikut adalah hokum-hukum yang berlaku pada aljabar bole.

1. Hukum Komutatif
A + B = A + A
A . B = B . A

2. Hukum Distributif
A( B + C) = AB + AC
A + BC = ( A + B) . ( A + C)

3. Hukum Asosiatif
( A + B ) + C = A + ( B + C)
(A . B) C =  A ( B. C)

4. Hukum Redundansi
A + AB = A A+A’B=A+B
A . (A + B) = A

5. Hukum Negasi
A’ = A’
(A’)’ = A

6. Hukum Identitas
A + A = A
A + 0 = A
A . A = A
A · 1 = A

7. Hukum Komplementasi

A.A’=0

A+A’=1

8. Hukum penyalinan satu kostanta

A.1=A A+1=1 A.0=0 A+0=A

9. Hukum absorsi

A+(A.B)=A A(A+B)=A

10. Hukum Dmorgan

A.B=A’+B’ A’.B’=A+B

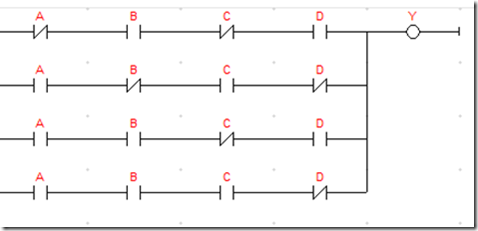
Berikut ini adalah contoh penyelesaian persamaan menggunakan aljabar boole untuk persamaan Y= A’.B.C’.D + A.B’.C.D’ + A.B.C’.D + A.B.C.D’ jika logika ini di konversi ke program ladder maka akan menjadi seperti berikut ini.

gambar 2.3. ladder diagram normal

namun dapat lebih sederhana jika menggunakan aljabar boole,berikut caranya

1. Carilah dua persamaan dengan 1 perbedaan

Y= A’.B.C’.D + A.B’.C.D’ + A.B.C’.D + A.B.C.D’

Y= {A’.B.C’D+ABC’D}+{A.B’.C.D’+A.B.C.D’}

Nilai A berbeda Nilai B berbeda

2. Lakukan perluasan persamaan

Y= {B.C’D(A’+A)}+{A.C.D’(B’+B) } lihat hukum komplementasi

Y= {B.C’D(1)}+{A.C.D’(1) }

Y= B.C’D+A.C.D’

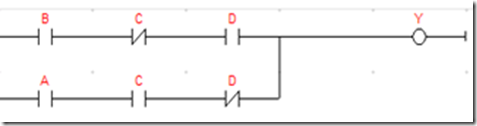
jadi diperoleh penyederhanaan menjadi Y= B.C’D+A.C.D’, dengan begitu kita dapat membuat ladder diagram yang lebih sederhana seperti pada gambar 2.4.

Gambar 2.4 Ladder penyederhanaan Aljabar Boole